 ¶
¶
Atmospheric Toolbox - Basics of HARP functionalities¶
In this example some of the basic functionalities of the ESA Atmospheric Toolbox to handle TROPOMI data are demonstrated. This case focuses on the use of toolbox's HARP component in Python, implemented as a Jupyter notebook.
The ESA Copernicus TROPOMI instrument onboard Sentinel 5p satellite observes atmospheric constituents at very high spatial resolution. In this tutorial we will demonstrate basic data reading and plotting procedures using TROPOMI SO2 observations. We use observations that were obtained during the explosive eruption of La Soufriere volcano in the Caribbean in April 2021. The eruption released large amounts of SO2 into the atmosphere, resulting extensive volcanic SO2 plumes that were transported long distances. This notebook will demonstrate how this event can be visualized using TROPOMI SO2 observations and HARP.
In the steps below this tutorial shows
- basic data reading using HARP
- how to plot single orbit TROPOMI data on a map, and
- how to apply operations to the TROPOMI data when importing with HARP
Initial preparations¶
To follow this notebook some preparations are needed. The TROPOMI SO2 data used in this notebook is obtained from the Copernicus Data Space Ecosystem.
This example uses the following TROPOMI SO2 file obtained at 12.4.2021:
S5P_RPRO_L2__SO2____20210412T151823_20210412T165953_18121_03_020401_20230209T050738.nc
In addition to HARP, this notebook uses several other Python packages that needs to be installed beforehand. The packages needed for running the notebook are:
- harp: for reading and handling of TROPOMI data
- numpy: for working with arrays
- matplotlib: for visualizing data
- cartopy: for geospatial data processing, e.g. for plotting maps
- cmcrameri: for universally readable scientific colormaps
The instructions on how to get started with the Atmospheric toolbox using Python and install HARP can be found here (add link to getting started jupyter notebook). Please note that if you have installed HARP in some specific python environment, check that you have activated the environment before running the script.
Step1: Reading TROPOMI SO2 data using HARP¶
First the needed Python packages are imported; harp, numpy, matplotlib, cartopy, and cmcrameri:
import os
import harp
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize
import cartopy.crs as ccrs
from cmcrameri import cm
import eofetch
The second step is to import the TROPOMI Level 2 SO2 file using harp.import_product(). If the file does not yet exist on your local machine, we use the avl library to automatically download the file from the Copernicus Dataspace Ecosystem (CDSE). (Because the original netcdf file is large, both downloading and importing the file might take a while.)
filename = "S5P_RPRO_L2__SO2____20210412T151823_20210412T165953_18121_03_020401_20230209T050738.nc"
We use eofetch to download the S5P product. To be able to perform the download yourself you will need to retrieve and configure credentials as described in the eofetch README. Alternatively, you can download the file manually and put it in the same directory as this notebook.
eofetch.download(filename)
product = harp.import_product(filename)
After a successful import, you have created a python variable called product. The variable product contains a record of the SO2 product variables, the data is imported as numpy arrays. You can view the contents of product using the Python print() function:
print(product)
source product = 'S5P_RPRO_L2__SO2____20210412T151823_20210412T165953_18121_03_020401_20230209T050738.nc'
int scan_subindex {time=1877400}
double datetime_start {time=1877400} [seconds since 2010-01-01]
float datetime_length [s]
long orbit_index
long validity {time=1877400}
float latitude {time=1877400} [degree_north]
float longitude {time=1877400} [degree_east]
float latitude_bounds {time=1877400, 4} [degree_north]
float longitude_bounds {time=1877400, 4} [degree_east]
float sensor_latitude {time=1877400} [degree_north]
float sensor_longitude {time=1877400} [degree_east]
float sensor_altitude {time=1877400} [m]
float solar_zenith_angle {time=1877400} [degree]
float solar_azimuth_angle {time=1877400} [degree]
float sensor_zenith_angle {time=1877400} [degree]
float sensor_azimuth_angle {time=1877400} [degree]
double pressure {time=1877400, vertical=34} [Pa]
float SO2_column_number_density {time=1877400} [mol/m^2]
float SO2_column_number_density_uncertainty_random {time=1877400} [mol/m^2]
float SO2_column_number_density_uncertainty_systematic {time=1877400} [mol/m^2]
byte SO2_column_number_density_validity {time=1877400}
float SO2_column_number_density_amf {time=1877400} []
float SO2_column_number_density_amf_uncertainty_random {time=1877400} []
float SO2_column_number_density_amf_uncertainty_systematic {time=1877400} []
float SO2_column_number_density_avk {time=1877400, vertical=34} []
float SO2_volume_mixing_ratio_dry_air_apriori {time=1877400, vertical=34} [ppv]
float SO2_slant_column_number_density {time=1877400} [mol/m^2]
byte SO2_type {time=1877400}
float O3_column_number_density {time=1877400} [mol/m^2]
float O3_column_number_density_uncertainty {time=1877400} [mol/m^2]
float absorbing_aerosol_index {time=1877400} []
float cloud_albedo {time=1877400} []
float cloud_albedo_uncertainty {time=1877400} []
float cloud_fraction {time=1877400} []
float cloud_fraction_uncertainty {time=1877400} []
float cloud_height {time=1877400} [km]
float cloud_height_uncertainty {time=1877400} [km]
float cloud_pressure {time=1877400} [Pa]
float cloud_pressure_uncertainty {time=1877400} [Pa]
float surface_albedo {time=1877400} []
float surface_altitude {time=1877400} [m]
float surface_altitude_uncertainty {time=1877400} [m]
float surface_pressure {time=1877400} [Pa]
float surface_meridional_wind_velocity {time=1877400} [m/s]
float surface_zonal_wind_velocity {time=1877400} [m/s]
double tropopause_pressure {time=1877400} [Pa]
long index {time=1877400}
With print command you can also inspect the information of a specific SO2 product variable (listed above), e.g. by typing:
print(product.SO2_column_number_density)
type = float
dimension = {time=1877400}
unit = 'mol/m^2'
valid_min = -inf
valid_max = inf
description = 'SO2 vertical column density'
data =
[nan nan nan ... nan nan nan]
From the listing above you see e.g. that the unit of the SO2_column_number_density variable is mol/m^2. Type of the product and the shape (size) of the SO2_column_number_density data array can be checked with the following commands:
print(type(product.SO2_column_number_density.data))
print(product.SO2_column_number_density.data.shape)
<class 'numpy.ndarray'> (1877400,)
Here it is important to notice that harp.import_product command imports and converts the TROPOMI Level 2 data to a structure that is compatible with the HARP conventions. This HARP compatible structure is different from the netcdf file structure. This HARP conversion includes e.g. restructuring data dimensions or renaming variables. For example, from the print commands above it is shown that after HARP import the dimension of the SO2_column_number_density data is time (=1877400), whereas working with netcdf-files directly using e.g. a library such as netCDF4, the dimensions of the same data field would be a 2D array, having Lat x Lon dimension.
HARP has builtin converters for a lot of atmospheric data products. For each conversion the HARP documentation contains a description of the variables it will return and how it mapped them from the original product format. The description for the TROPOMI SO2 product can be found here.
HARP does this conversion such that data from other satellite data products, such as OMI, or GOME-2, will end up having the same structure and naming conventions. This makes it a lot easier for users to deal with data coming from different satellite instruments.
Step 2: Plotting a single orbit data on a map¶
Now that the TROPOMI SO2 data product is imported, the data will be visualized on a map. The parameter we want to plot is the "SO2_column_number_density", which gives the total atmospheric SO2 column. For this we will be using cartopy and the scatter function. This plotting function is based on using only the pixel center coordinates of the satellite data, and not the actual latitude and longitude bounds. The scatter function will plot each satellite pixel as coloured single dot on a map based on their lat and lon coordinates. Cartopy also provides other plotting options, such as pcolormesh. However, in pcolormesh the input data needs to be a 2D array. This type of plotting will be demonstrated in the another use cases.
First, the SO2, latitude and longitude center data are defined. In addition, units and description of the SO2 data are read that are needed for the colorbar label. For plotting a colormap named "batlow" is chosen from the cmcrameri library. The cmcrameri provides scientific colormaps where the colour combinations are readable both by colour-vision deficient and colour-blind people. The Crameri colormap options can be viewed here. In the script the colormaps are called e.g. as cm.batlow. If you wish to use reversed colormap, append _r to the colormaps name. With vmin and vmax the scaling of the colormap values are defined.
SO2val = product.SO2_column_number_density.data
SO2units = product.SO2_column_number_density.unit
SO2description = product.SO2_column_number_density.description
latc=product.latitude.data
lonc=product.longitude.data
colortable=cm.batlow
vmin=0
vmax=0.0001
Next the figure properties will be defined. By using matplotlib figsize argument the figure size can be defined, plt.axes(projection=ccrs.PlateCarree()) sets a up GeoAxes instance, and ax.coastlines() adds the coastlines to the map. The actual data is plotted with plt.scatter command, where lat and lon coordinates are given as input, and the dots are coloured according to the pixel SO2 value (SO2val).
fig=plt.figure(figsize=(20, 10))
ax = plt.axes(projection=ccrs.PlateCarree())
img = plt.scatter(lonc, latc, c=SO2val,
vmin=vmin, vmax=vmax, cmap=colortable, s=1, transform=ccrs.PlateCarree())
ax.coastlines()
cbar = fig.colorbar(img, ax=ax, orientation='horizontal', fraction=0.04, pad=0.1)
cbar.set_label(f'{SO2description} [{SO2units}]')
cbar.ax.tick_params(labelsize=14)
plt.show()
Step 3: Applying operations when importing data with HARP¶
In the previous blocks one orbit of TROPOMI SO2 data has been imported with HARP and plotted on a map as it is. However, there is one very important step missing that is essential to apply when working with almost any satellite data: the quality flag(s). To ensure that you work with only good quality data and make correct interpretations, it is essential that the recommendations given for each TROPOMI Level 2 data are followed.
One of the main features of HARP is the ability to perform operations as part of the data import.¶
This very unique feature of HARP allows you to apply different kind of operations on the data already when importing it, and hence, no post processing is needed. These operations can include e.g. cutting the data over certain area only, converting units, and of course applying the quality flags. Information on all operations that can be applied can be found in the HARP operations documentation.
Now, we will import the same data file as in Step 1, but now adding four different operations as a part of the import command:
we only ingest data that is between -20S and 40N degrees latitude
we only consider pixels for which the data quality is high enough. The basic quality flag in any TROPOMI Level 2 netcdf file is given as
qa_value. In the the Product Readme File for SO2 you can find, that the basic recommendation for SO2 data is to use only those pixels whereqa_value > 0.5. When HARP imports data, the quality values are interpreted as numbers between 0 and 100 (not 0 and 1), hence our limit in this case is 50. In HARP theqa_valueis renamed asSO2_column_number_density_validity. The list of variables in HARP product after ingestion of S5P TROPOMI SO2 product are found here.we limit the variables that we read to those that we need
we convert the unit of the tropospheric SO2 column number density to Dobson Units (DU) (instead of using mol/m2 in which the original data was stored)
All these operations will be performed by HARP while the data is being read, and before it is returned to Python.
In the following, the HARP operations that are performed when importing data are here given as "operations" variable, that includes each HARP operation (name, condition) as string. All the applied HARP operations are separated with ";" and finally joined together with join() command. With "keep" operation it is defined which variables from the original netcdf files are imported, while "derive" operation performs the conversion from original units to dobson units. After joining the operations together you can print the resulting string using the print() command. In Python defining an "operations" string parameter is a convenient way to define and keep track on different operations to be applied when importing the data. Other option would be to write the operations as an input to the HARP import command as: "operation1;operation2;operation3".
operations = ";".join([
"latitude>-20;latitude<40",
"SO2_column_number_density_validity>50",
"keep(datetime_start,scan_subindex,latitude,longitude,SO2_column_number_density)",
"derive(SO2_column_number_density [DU])",
])
print(type(operations))
print(operations)
<class 'str'> latitude>-20;latitude<40;SO2_column_number_density_validity>50;keep(datetime_start,scan_subindex,latitude,longitude,SO2_column_number_density);derive(SO2_column_number_density [DU])
The import with HARP including operations is executed with the same harp.import_product()command as before, but in addition to filename now also the "operations" variable is given as input, separated with a comma. We will call the new imported variable as "reduced_product":
reduced_product = harp.import_product(filename, operations)
You will see that importing the data now goes a lot faster. If we print the contents of the reduced_product, it shows that the variable consists only those parameters we requested, and the SO2 units are as DU. Also the time dimension of the data is less than in Step 1, because only those pixels between -20S-40N have been considered:
print(reduced_product)
source product = 'S5P_RPRO_L2__SO2____20210412T151823_20210412T165953_18121_03_020401_20230209T050738.nc'
history = "2024-05-17T14:33:21Z [harp-1.21] harp.import_product('S5P_RPRO_L2__SO2____20210412T151823_20210412T165953_18121_03_020401_20230209T050738.nc',operations='latitude>-20;latitude<40;SO2_column_number_density_validity>50;keep(datetime_start,scan_subindex,latitude,longitude,SO2_column_number_density);derive(SO2_column_number_density [DU])')"
int scan_subindex {time=455625}
double datetime_start {time=455625} [seconds since 2010-01-01]
float latitude {time=455625} [degree_north]
float longitude {time=455625} [degree_east]
double SO2_column_number_density {time=455625} [DU]
Now that the new reduced data is imported, the same approach as in Step 2 can be used to plot the data on a map. Note that now the units of SO2 have changed, and therefore different scaling for the colorscheme is needed. First define the parameters for plotting:
SO2val = reduced_product.SO2_column_number_density.data
SO2units = reduced_product.SO2_column_number_density.unit
SO2description = reduced_product.SO2_column_number_density.description
latc=reduced_product.latitude.data
lonc=reduced_product.longitude.data
colortable=cm.batlow
# For Dobson Units
vmin=0
vmax=8
And then plot the figure:
fig=plt.figure(figsize=(20, 10))
ax = plt.axes(projection=ccrs.PlateCarree())
img = plt.scatter(lonc, latc, c=SO2val,
vmin=vmin, vmax=vmax, cmap=colortable, s=1, transform=ccrs.PlateCarree())
ax.coastlines()
cbar = fig.colorbar(img, ax=ax, orientation='horizontal', fraction=0.04, pad=0.1)
cbar.set_label(f'{SO2description} [{SO2units}]')
cbar.ax.tick_params(labelsize=14)
plt.show()
The plot shows how the large SO2 plume originating from La Soufriere eruption extends across the orbit. There are now also white areas within the plume, where bad quality pixels have been filtered out. It is also noticeable now much faster the plotting procedure is with the reduced dataset.
Step 4: Regridding with HARP and plotting using pcolormesh¶
In Steps 2 and 3 we applied the scatter function for quick plotting, however, it is not an optimal function to visualize satellite data on a map, since each pixel is plotted as a single dot. The other plot function from cartopy is pcolormesh. However, the mesh plot requires the input data (latitude, longitude, and variable to plot) as 2D matrices, and therefore the pcolormesh can not be directly applied to data imported and filtered using HARP (Step 3). This is because after these filtering operations we don't have all pixels for a scanline anymore.
A solution to this problem is to regrid the S5P data to a regular latitude/longitude grid before plotting. The regridding can be done by using a bin_spatial() operation when importing data with HARP. Regridding data into a lat/lon grid is also needed if we want to combine the data from multiple orbits from one day into a single daily grid. This will be demonstrated in another use case.
The bin_spatial() operation requires six input parameters, that defines the new grid. The input parameters are:
- the number of latitude edge points
- the latitude offset at which to start the grid
- the latitude increment (= latitude length of a grid cell)
- the number of longitude edge points
- the longitude offset at which to start the grid
- the longitude increment (= longitude length of a grid cell)
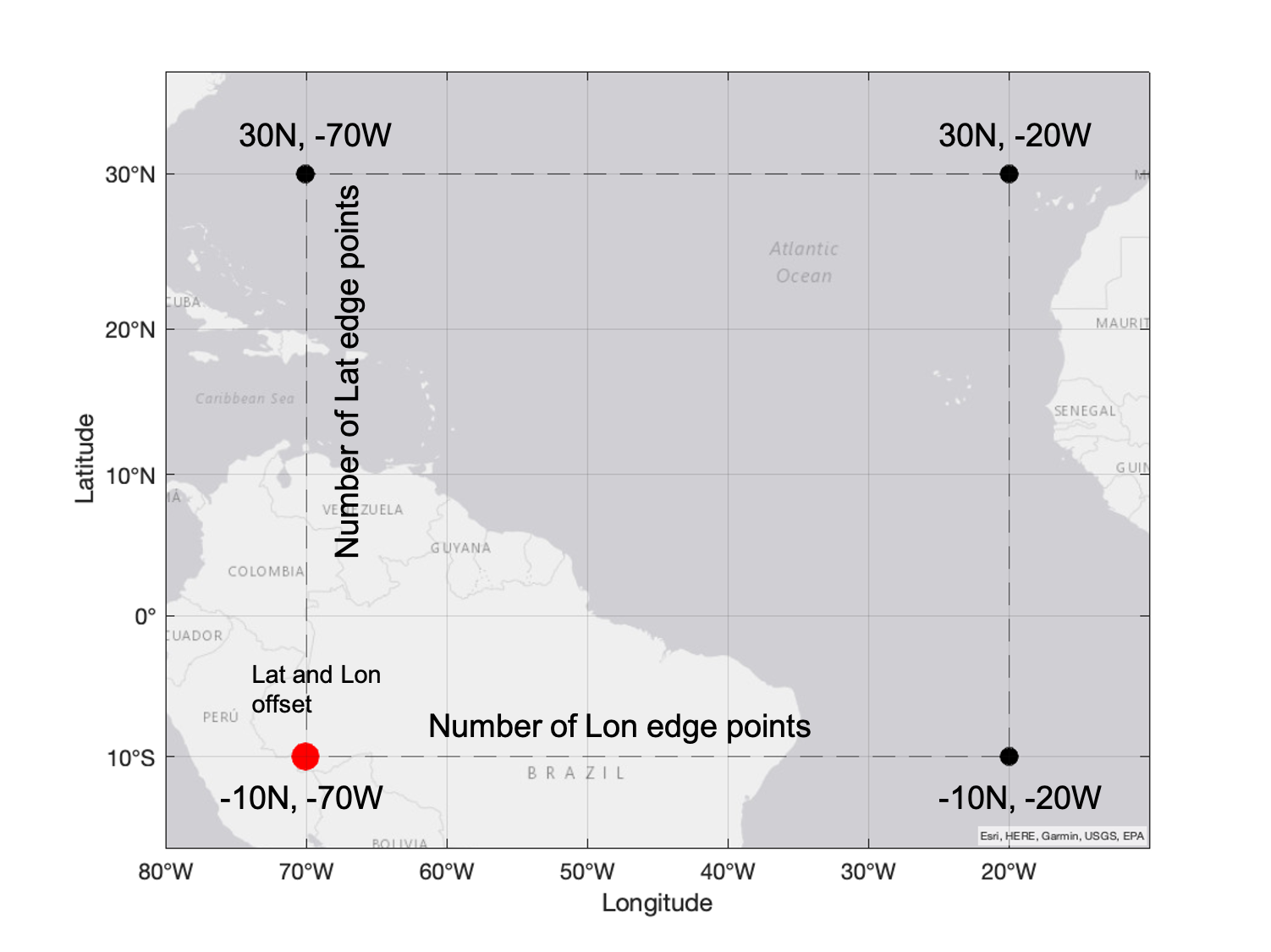
In this example we define a new grid at 0.05 degrees resolution over the area of the volcanic SO2 plume. The latitude and longitude offset in this case is for latitude -10S, and for longitude -70W (red point in the picture). Since the grid resolution is now 0.05 degrees and the latitudes in the new grid extend from -10S to 30N, the number of latitude edge points is 801 (=number of points from -10 to 30 at 0.05 steps). Similarly, since the the longitudes in the grid extend from -70W to -20W, the number of longitude edge points is 1001. Hence, the number edge points is one more than the number of grid cells. This is similar to the way you should provide the X and Y parameters to the pcolormesh function (see matplotlib_documentation).
For a 0.1 degree by 0.1 degree global grid we would need 1800 by 3600 grid cells which equals 1801 by 3601 grid edge points.
The input for bin_spatial() is given in the following order:
bin_spatial(lat_edge_length, lat_edge_offset, lat_edge_step, lon_edge_length, lon_edge_offset, lon_edge_step)
In this example, the bin_spatial() input is:
bin_spatial(801, -10, 0.05, 1001, -70, 0.05)
HARP can actually do a proper weighted area average to calculate the value for each grid cell. It will need the corner coordinates of each satellite pixel, provided by the latitude_bounds and longitude_bounds. This is why we need to add these variables to the keep() operation we perform below. We also add derive() latitude and longitude, so that the new grid center coordinates are included in the imported variable.
As a summary, in this example the operations that will be performed with HARP import are:
- considering only good quality SO2 observations: "SO2_column_number_density_validity>50"
- keeping the needed parameters: "keep(latitude_bounds,longitude_bounds,SO2_column_number_density)"
- regridding the SO2 data: "bin_spatial(801, -10, 0.05, 1001, -70, 0.05)"
- converting SO2 to Dobson Units: "derive(SO2_column_number_density [DU])"
- derive latitude and longitude coordinates of the new grid: "derive(latitude {latitude})","derive(longitude {longitude})"
operations = ";".join([
"SO2_column_number_density_validity>50",
"keep(latitude_bounds,longitude_bounds,SO2_column_number_density)",
"bin_spatial(801, -10, 0.05, 1001, -70, 0.05)",
"derive(SO2_column_number_density [DU])",
"derive(latitude {latitude})",
"derive(longitude {longitude})",
])
Here the new regridded variable is named as "regridded_product". The content of the "regridded_product" can be viewed using the Python print() command.
regridded_product = harp.import_product(filename, operations)
print(regridded_product)
source product = 'S5P_RPRO_L2__SO2____20210412T151823_20210412T165953_18121_03_020401_20230209T050738.nc'
history = "2024-05-17T14:33:27Z [harp-1.21] harp.import_product('S5P_RPRO_L2__SO2____20210412T151823_20210412T165953_18121_03_020401_20230209T050738.nc',operations='SO2_column_number_density_validity>50;keep(latitude_bounds,longitude_bounds,SO2_column_number_density);bin_spatial(801, -10, 0.05, 1001, -70, 0.05);derive(SO2_column_number_density [DU]);derive(latitude {latitude});derive(longitude {longitude})')"
double SO2_column_number_density {time=1, latitude=800, longitude=1000} [DU]
long count {time=1}
float weight {time=1, latitude=800, longitude=1000}
double latitude_bounds {latitude=800, 2} [degree_north]
double longitude_bounds {longitude=1000, 2} [degree_east]
double latitude {latitude=800} [degree_north]
double longitude {longitude=1000} [degree_east]
As the printing of variables show, the re-gridded SO2 variable has now two dimensions (in addition to time), latitude (800) and longitude (1000). Hence, now it is possible to use pcolormesh function since the SO2_column_number_density is a 2D array.
The corner coordinates of each grid cell are provided by the latitude_bounds and longitude_bounds variables and these are used for plotting. Note that the pcolormesh function requires these corner coordinates as the input for latitude and longitude. As we see from the print above, the shape (dimensions) of latitude_bounds and longitude_bounds is 1000 x 2. The regridded_product.latitude_bounds.data[:,0] array gives the latitudes of the lower corners, whereas regridded_product.latitude_bounds.data[:,1] gives the latitudes for upper corners.
print(regridded_product.latitude_bounds.data[:,0])
print(regridded_product.latitude_bounds.data[:,1])
[-10. -9.95 -9.9 -9.85 -9.8 -9.75 -9.7 -9.65 -9.6 -9.55 -9.5 -9.45 -9.4 -9.35 -9.3 -9.25 -9.2 -9.15 -9.1 -9.05 -9. -8.95 -8.9 -8.85 -8.8 -8.75 -8.7 -8.65 -8.6 -8.55 -8.5 -8.45 -8.4 -8.35 -8.3 -8.25 -8.2 -8.15 -8.1 -8.05 -8. -7.95 -7.9 -7.85 -7.8 -7.75 -7.7 -7.65 -7.6 -7.55 -7.5 -7.45 -7.4 -7.35 -7.3 -7.25 -7.2 -7.15 -7.1 -7.05 -7. -6.95 -6.9 -6.85 -6.8 -6.75 -6.7 -6.65 -6.6 -6.55 -6.5 -6.45 -6.4 -6.35 -6.3 -6.25 -6.2 -6.15 -6.1 -6.05 -6. -5.95 -5.9 -5.85 -5.8 -5.75 -5.7 -5.65 -5.6 -5.55 -5.5 -5.45 -5.4 -5.35 -5.3 -5.25 -5.2 -5.15 -5.1 -5.05 -5. -4.95 -4.9 -4.85 -4.8 -4.75 -4.7 -4.65 -4.6 -4.55 -4.5 -4.45 -4.4 -4.35 -4.3 -4.25 -4.2 -4.15 -4.1 -4.05 -4. -3.95 -3.9 -3.85 -3.8 -3.75 -3.7 -3.65 -3.6 -3.55 -3.5 -3.45 -3.4 -3.35 -3.3 -3.25 -3.2 -3.15 -3.1 -3.05 -3. -2.95 -2.9 -2.85 -2.8 -2.75 -2.7 -2.65 -2.6 -2.55 -2.5 -2.45 -2.4 -2.35 -2.3 -2.25 -2.2 -2.15 -2.1 -2.05 -2. -1.95 -1.9 -1.85 -1.8 -1.75 -1.7 -1.65 -1.6 -1.55 -1.5 -1.45 -1.4 -1.35 -1.3 -1.25 -1.2 -1.15 -1.1 -1.05 -1. -0.95 -0.9 -0.85 -0.8 -0.75 -0.7 -0.65 -0.6 -0.55 -0.5 -0.45 -0.4 -0.35 -0.3 -0.25 -0.2 -0.15 -0.1 -0.05 0. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1. 1.05 1.1 1.15 1.2 1.25 1.3 1.35 1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9 1.95 2. 2.05 2.1 2.15 2.2 2.25 2.3 2.35 2.4 2.45 2.5 2.55 2.6 2.65 2.7 2.75 2.8 2.85 2.9 2.95 3. 3.05 3.1 3.15 3.2 3.25 3.3 3.35 3.4 3.45 3.5 3.55 3.6 3.65 3.7 3.75 3.8 3.85 3.9 3.95 4. 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4 4.45 4.5 4.55 4.6 4.65 4.7 4.75 4.8 4.85 4.9 4.95 5. 5.05 5.1 5.15 5.2 5.25 5.3 5.35 5.4 5.45 5.5 5.55 5.6 5.65 5.7 5.75 5.8 5.85 5.9 5.95 6. 6.05 6.1 6.15 6.2 6.25 6.3 6.35 6.4 6.45 6.5 6.55 6.6 6.65 6.7 6.75 6.8 6.85 6.9 6.95 7. 7.05 7.1 7.15 7.2 7.25 7.3 7.35 7.4 7.45 7.5 7.55 7.6 7.65 7.7 7.75 7.8 7.85 7.9 7.95 8. 8.05 8.1 8.15 8.2 8.25 8.3 8.35 8.4 8.45 8.5 8.55 8.6 8.65 8.7 8.75 8.8 8.85 8.9 8.95 9. 9.05 9.1 9.15 9.2 9.25 9.3 9.35 9.4 9.45 9.5 9.55 9.6 9.65 9.7 9.75 9.8 9.85 9.9 9.95 10. 10.05 10.1 10.15 10.2 10.25 10.3 10.35 10.4 10.45 10.5 10.55 10.6 10.65 10.7 10.75 10.8 10.85 10.9 10.95 11. 11.05 11.1 11.15 11.2 11.25 11.3 11.35 11.4 11.45 11.5 11.55 11.6 11.65 11.7 11.75 11.8 11.85 11.9 11.95 12. 12.05 12.1 12.15 12.2 12.25 12.3 12.35 12.4 12.45 12.5 12.55 12.6 12.65 12.7 12.75 12.8 12.85 12.9 12.95 13. 13.05 13.1 13.15 13.2 13.25 13.3 13.35 13.4 13.45 13.5 13.55 13.6 13.65 13.7 13.75 13.8 13.85 13.9 13.95 14. 14.05 14.1 14.15 14.2 14.25 14.3 14.35 14.4 14.45 14.5 14.55 14.6 14.65 14.7 14.75 14.8 14.85 14.9 14.95 15. 15.05 15.1 15.15 15.2 15.25 15.3 15.35 15.4 15.45 15.5 15.55 15.6 15.65 15.7 15.75 15.8 15.85 15.9 15.95 16. 16.05 16.1 16.15 16.2 16.25 16.3 16.35 16.4 16.45 16.5 16.55 16.6 16.65 16.7 16.75 16.8 16.85 16.9 16.95 17. 17.05 17.1 17.15 17.2 17.25 17.3 17.35 17.4 17.45 17.5 17.55 17.6 17.65 17.7 17.75 17.8 17.85 17.9 17.95 18. 18.05 18.1 18.15 18.2 18.25 18.3 18.35 18.4 18.45 18.5 18.55 18.6 18.65 18.7 18.75 18.8 18.85 18.9 18.95 19. 19.05 19.1 19.15 19.2 19.25 19.3 19.35 19.4 19.45 19.5 19.55 19.6 19.65 19.7 19.75 19.8 19.85 19.9 19.95 20. 20.05 20.1 20.15 20.2 20.25 20.3 20.35 20.4 20.45 20.5 20.55 20.6 20.65 20.7 20.75 20.8 20.85 20.9 20.95 21. 21.05 21.1 21.15 21.2 21.25 21.3 21.35 21.4 21.45 21.5 21.55 21.6 21.65 21.7 21.75 21.8 21.85 21.9 21.95 22. 22.05 22.1 22.15 22.2 22.25 22.3 22.35 22.4 22.45 22.5 22.55 22.6 22.65 22.7 22.75 22.8 22.85 22.9 22.95 23. 23.05 23.1 23.15 23.2 23.25 23.3 23.35 23.4 23.45 23.5 23.55 23.6 23.65 23.7 23.75 23.8 23.85 23.9 23.95 24. 24.05 24.1 24.15 24.2 24.25 24.3 24.35 24.4 24.45 24.5 24.55 24.6 24.65 24.7 24.75 24.8 24.85 24.9 24.95 25. 25.05 25.1 25.15 25.2 25.25 25.3 25.35 25.4 25.45 25.5 25.55 25.6 25.65 25.7 25.75 25.8 25.85 25.9 25.95 26. 26.05 26.1 26.15 26.2 26.25 26.3 26.35 26.4 26.45 26.5 26.55 26.6 26.65 26.7 26.75 26.8 26.85 26.9 26.95 27. 27.05 27.1 27.15 27.2 27.25 27.3 27.35 27.4 27.45 27.5 27.55 27.6 27.65 27.7 27.75 27.8 27.85 27.9 27.95 28. 28.05 28.1 28.15 28.2 28.25 28.3 28.35 28.4 28.45 28.5 28.55 28.6 28.65 28.7 28.75 28.8 28.85 28.9 28.95 29. 29.05 29.1 29.15 29.2 29.25 29.3 29.35 29.4 29.45 29.5 29.55 29.6 29.65 29.7 29.75 29.8 29.85 29.9 29.95] [-9.95 -9.9 -9.85 -9.8 -9.75 -9.7 -9.65 -9.6 -9.55 -9.5 -9.45 -9.4 -9.35 -9.3 -9.25 -9.2 -9.15 -9.1 -9.05 -9. -8.95 -8.9 -8.85 -8.8 -8.75 -8.7 -8.65 -8.6 -8.55 -8.5 -8.45 -8.4 -8.35 -8.3 -8.25 -8.2 -8.15 -8.1 -8.05 -8. -7.95 -7.9 -7.85 -7.8 -7.75 -7.7 -7.65 -7.6 -7.55 -7.5 -7.45 -7.4 -7.35 -7.3 -7.25 -7.2 -7.15 -7.1 -7.05 -7. -6.95 -6.9 -6.85 -6.8 -6.75 -6.7 -6.65 -6.6 -6.55 -6.5 -6.45 -6.4 -6.35 -6.3 -6.25 -6.2 -6.15 -6.1 -6.05 -6. -5.95 -5.9 -5.85 -5.8 -5.75 -5.7 -5.65 -5.6 -5.55 -5.5 -5.45 -5.4 -5.35 -5.3 -5.25 -5.2 -5.15 -5.1 -5.05 -5. -4.95 -4.9 -4.85 -4.8 -4.75 -4.7 -4.65 -4.6 -4.55 -4.5 -4.45 -4.4 -4.35 -4.3 -4.25 -4.2 -4.15 -4.1 -4.05 -4. -3.95 -3.9 -3.85 -3.8 -3.75 -3.7 -3.65 -3.6 -3.55 -3.5 -3.45 -3.4 -3.35 -3.3 -3.25 -3.2 -3.15 -3.1 -3.05 -3. -2.95 -2.9 -2.85 -2.8 -2.75 -2.7 -2.65 -2.6 -2.55 -2.5 -2.45 -2.4 -2.35 -2.3 -2.25 -2.2 -2.15 -2.1 -2.05 -2. -1.95 -1.9 -1.85 -1.8 -1.75 -1.7 -1.65 -1.6 -1.55 -1.5 -1.45 -1.4 -1.35 -1.3 -1.25 -1.2 -1.15 -1.1 -1.05 -1. -0.95 -0.9 -0.85 -0.8 -0.75 -0.7 -0.65 -0.6 -0.55 -0.5 -0.45 -0.4 -0.35 -0.3 -0.25 -0.2 -0.15 -0.1 -0.05 0. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1. 1.05 1.1 1.15 1.2 1.25 1.3 1.35 1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9 1.95 2. 2.05 2.1 2.15 2.2 2.25 2.3 2.35 2.4 2.45 2.5 2.55 2.6 2.65 2.7 2.75 2.8 2.85 2.9 2.95 3. 3.05 3.1 3.15 3.2 3.25 3.3 3.35 3.4 3.45 3.5 3.55 3.6 3.65 3.7 3.75 3.8 3.85 3.9 3.95 4. 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4 4.45 4.5 4.55 4.6 4.65 4.7 4.75 4.8 4.85 4.9 4.95 5. 5.05 5.1 5.15 5.2 5.25 5.3 5.35 5.4 5.45 5.5 5.55 5.6 5.65 5.7 5.75 5.8 5.85 5.9 5.95 6. 6.05 6.1 6.15 6.2 6.25 6.3 6.35 6.4 6.45 6.5 6.55 6.6 6.65 6.7 6.75 6.8 6.85 6.9 6.95 7. 7.05 7.1 7.15 7.2 7.25 7.3 7.35 7.4 7.45 7.5 7.55 7.6 7.65 7.7 7.75 7.8 7.85 7.9 7.95 8. 8.05 8.1 8.15 8.2 8.25 8.3 8.35 8.4 8.45 8.5 8.55 8.6 8.65 8.7 8.75 8.8 8.85 8.9 8.95 9. 9.05 9.1 9.15 9.2 9.25 9.3 9.35 9.4 9.45 9.5 9.55 9.6 9.65 9.7 9.75 9.8 9.85 9.9 9.95 10. 10.05 10.1 10.15 10.2 10.25 10.3 10.35 10.4 10.45 10.5 10.55 10.6 10.65 10.7 10.75 10.8 10.85 10.9 10.95 11. 11.05 11.1 11.15 11.2 11.25 11.3 11.35 11.4 11.45 11.5 11.55 11.6 11.65 11.7 11.75 11.8 11.85 11.9 11.95 12. 12.05 12.1 12.15 12.2 12.25 12.3 12.35 12.4 12.45 12.5 12.55 12.6 12.65 12.7 12.75 12.8 12.85 12.9 12.95 13. 13.05 13.1 13.15 13.2 13.25 13.3 13.35 13.4 13.45 13.5 13.55 13.6 13.65 13.7 13.75 13.8 13.85 13.9 13.95 14. 14.05 14.1 14.15 14.2 14.25 14.3 14.35 14.4 14.45 14.5 14.55 14.6 14.65 14.7 14.75 14.8 14.85 14.9 14.95 15. 15.05 15.1 15.15 15.2 15.25 15.3 15.35 15.4 15.45 15.5 15.55 15.6 15.65 15.7 15.75 15.8 15.85 15.9 15.95 16. 16.05 16.1 16.15 16.2 16.25 16.3 16.35 16.4 16.45 16.5 16.55 16.6 16.65 16.7 16.75 16.8 16.85 16.9 16.95 17. 17.05 17.1 17.15 17.2 17.25 17.3 17.35 17.4 17.45 17.5 17.55 17.6 17.65 17.7 17.75 17.8 17.85 17.9 17.95 18. 18.05 18.1 18.15 18.2 18.25 18.3 18.35 18.4 18.45 18.5 18.55 18.6 18.65 18.7 18.75 18.8 18.85 18.9 18.95 19. 19.05 19.1 19.15 19.2 19.25 19.3 19.35 19.4 19.45 19.5 19.55 19.6 19.65 19.7 19.75 19.8 19.85 19.9 19.95 20. 20.05 20.1 20.15 20.2 20.25 20.3 20.35 20.4 20.45 20.5 20.55 20.6 20.65 20.7 20.75 20.8 20.85 20.9 20.95 21. 21.05 21.1 21.15 21.2 21.25 21.3 21.35 21.4 21.45 21.5 21.55 21.6 21.65 21.7 21.75 21.8 21.85 21.9 21.95 22. 22.05 22.1 22.15 22.2 22.25 22.3 22.35 22.4 22.45 22.5 22.55 22.6 22.65 22.7 22.75 22.8 22.85 22.9 22.95 23. 23.05 23.1 23.15 23.2 23.25 23.3 23.35 23.4 23.45 23.5 23.55 23.6 23.65 23.7 23.75 23.8 23.85 23.9 23.95 24. 24.05 24.1 24.15 24.2 24.25 24.3 24.35 24.4 24.45 24.5 24.55 24.6 24.65 24.7 24.75 24.8 24.85 24.9 24.95 25. 25.05 25.1 25.15 25.2 25.25 25.3 25.35 25.4 25.45 25.5 25.55 25.6 25.65 25.7 25.75 25.8 25.85 25.9 25.95 26. 26.05 26.1 26.15 26.2 26.25 26.3 26.35 26.4 26.45 26.5 26.55 26.6 26.65 26.7 26.75 26.8 26.85 26.9 26.95 27. 27.05 27.1 27.15 27.2 27.25 27.3 27.35 27.4 27.45 27.5 27.55 27.6 27.65 27.7 27.75 27.8 27.85 27.9 27.95 28. 28.05 28.1 28.15 28.2 28.25 28.3 28.35 28.4 28.45 28.5 28.55 28.6 28.65 28.7 28.75 28.8 28.85 28.9 28.95 29. 29.05 29.1 29.15 29.2 29.25 29.3 29.35 29.4 29.45 29.5 29.55 29.6 29.65 29.7 29.75 29.8 29.85 29.9 29.95 30. ]
As we see from the print, regridded_product.latitude_bounds.data[:,1] contains the j+1 coordinates of the first dimension ([:,0]) plus the upper right corner latitude of the grid. To get the correct input for pcolormesh, we define the gridlat variable by appending the regridded_product.latitude_bounds.data[:,0] array with the last element of the second array: regridded_product.longitude_bounds.data[-1,1]. The gridlon variable is defined similarly:
gridlat = np.append(regridded_product.latitude_bounds.data[:,0], regridded_product.latitude_bounds.data[-1,1])
gridlon = np.append(regridded_product.longitude_bounds.data[:,0], regridded_product.longitude_bounds.data[-1,1])
SO2val = regridded_product.SO2_column_number_density.data
SO2units = regridded_product.SO2_column_number_density.unit
SO2description = regridded_product.SO2_column_number_density.description
colortable=cm.batlow
# For Dobson Units
vmin=0
vmax=9
Next the figure properties are defined. In Steps 2 and 3 we used the scatter function, here the actual data is plotted with plt.pcolormesh command, having as an input gridlon, gridlat, SO2 value and the colormap definitions. Note that the dimensions of the SO2val are time, lat, and lon, and therefore the input is given as SO2val[0,:,:]. Finally the colorbar is added with label text, and also the location of the colorbar is set.
fig = plt.figure(figsize=(20,10))
ax = plt.axes(projection=ccrs.PlateCarree())
img = plt.pcolormesh(gridlon, gridlat, SO2val[0,:,:], vmin=vmin, vmax=vmax,
cmap=colortable, transform=ccrs.PlateCarree())
ax.coastlines()
ax.gridlines()
cbar = fig.colorbar(img, ax=ax,orientation='horizontal', fraction=0.04, pad=0.1)
cbar.set_label(f'{SO2description}[{SO2units}]')
cbar.ax.tick_params(labelsize=14)
plt.show()